نظريات المماس في الدائرة وتمارين محلولة .. خصائص مماس الدائرة
تعتبر نظرية المماس في الدائرة هي أحد العناصر الهامة في علم الرياضيات وبالتحديد قسم الهندسة والدوائر، حيث تُدرس هذه النوعية من المواد الدراسية في المدارس والجامعات بشكل مستمر لمختلف المراحل الدراسية، لذلك من خلال موقع منصتك نقدم لكم نظريات المماس في الدائرة وتمارين محلولة للشرح وتسهيل المعلومة.
نظريات المماس في الدائرة
يُعرف مماس الدائرة في علم الرياضيات على إنه ظل الدائرة والذي يُعد خط مستقيم يقع خارج الدائرة ولكن يلامسها عند نقطة واحدة فقط.
وتسمى هذه النقطة التي يتلامس بها الخط مع الدائرة هو مماس الدائرة، أي هي نقطة التماس بشكل أصح والتي يكون عندها المماس عمودي على نصف القطر بشكل دائم.
تعتبر هذه النظرية من العناصر الهامة التي يتم تدريسها في الإنشاءات والبراهين الهندسية وذلك لأن خط المماس يكون عمودي على نصف القطر والتي تتضمن دوائر متعامدة مع خطوط شعاعية.
اقرأ أيضًا: ما هي نظريات الإعلام الجديد .. التحديات التي تواجه الإعلام الجديد
خصائص مماس الدائرة
يضم تعريف مماس الدائرة عدد من الخصائص الهامة والتي يجب العناية بها عند دراسة هذا المفهوم، ومن خلال النقاط التالية نوضح لكم خصائص مماس الدائرة بالتفصيل:
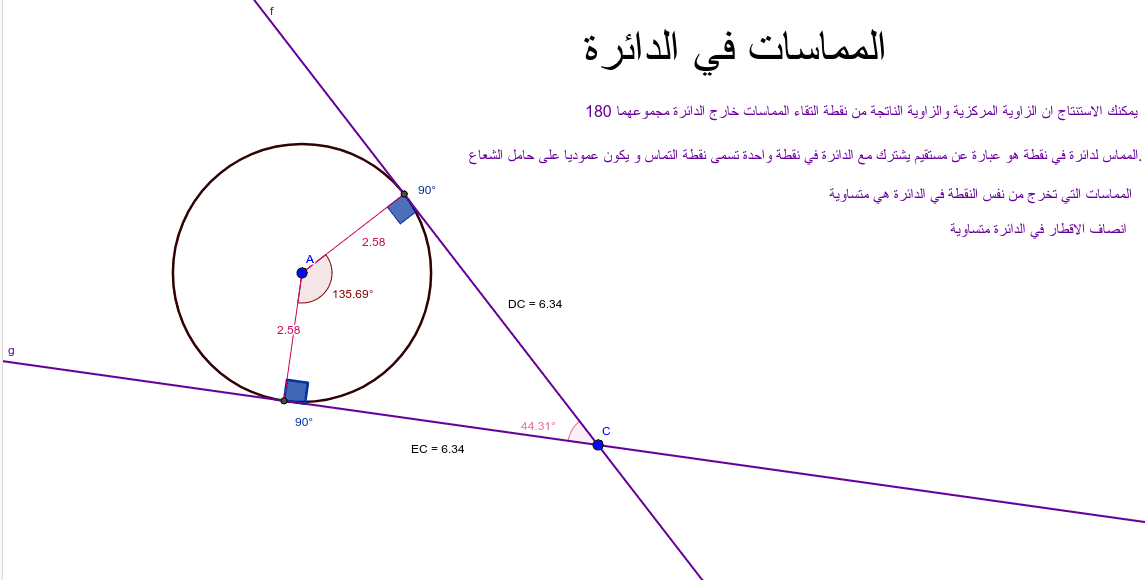
- تكون أطوال المماس المنطلقة من نقطة خارجية مشتركة إلى الدائرة متساوية.
- لا يتقاطع خط المماس مع الدائرة بل يلمسها فقط.
- يكون المماس عمودي على نصف القطر عند نقطة التماس.
- يتلامس المماس الدائرة عند نقطة واحدة فقط.
- يؤدي قطر الدائرة إلى تقسيم الدائرة إلى قسمين بنفس الحجم.
اقرأ أيضًا: ما هي نظريات علم الجمال
حالات مماس الدائرة
تتضمن فكرة مماس الدائرة عدة حالات هامة يتم من خلالها تحديد مماس الدائرة تختلف باختلاف نقطة التماس وموقعه بالنسبة للدائرة، حيث تشمل حالات مماس الدائرة النقاط التالية:
- تواجد النقطة على الدائرة والتي تكون مماس واحد مع النقطة على محيط الدائرة.
- تواجد النقطة خارج الدائرة والتي ينطلق بها خارج الدائرة ويلمس الدائرة عند نقطة واحدة فقط.
اقرأ أيضًا: نظريات الاتصال والتأثير غير المباشر
تمارين محلولة عن نظرية المماس
نوضح لكم من خلال المثال التالي تمرين محلول عن نظرية مماس الدائرة والتي يتم شرحها وتدريسها في المدارس لمختلف المراحل العمرية، حيث تشمل هذه التمارين ما يلي:
دائرة معادلتها (س² + ص² = 25)، أوجد معادلة المماس إذا علمت أن إحداثيّات نقطة التماس هي (3، -4):
خطوات الحل: نستنتج من معادلة الدائرة أن إحداثيّات نقطة المركز هي (0،0) ونصف القطر يساوي 5. نجد ميل نصف القطر = -4/ 3 نجد ميل المماس = 3/ 4 نعوض كل من ميل المماس وإحداثيّات نقطة التماس في معادلة المماس بحيث تصبح المعادلة (ص + 4) = (3/ 4) (س – 3)
لقد وفرنا لكم من خلال هذا المقال كل التفاصيل والمعلومات عن مماس الدائرة وذلك من حيث تقديم شرح مستوفي عن مفهوم النظرية وكذلك خصائص عن حالة المماس مع شرح مستوفي لحالات المماس وتمارين محلولة مع أمثلة عن نظرية المماس والتي يتم تدريسها في كافة المدارس والجامعات.